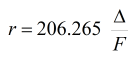
To determine the resolution of an image from the characteristics of the instruments there is a known formula:

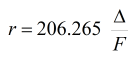
where r is the resolution (in "/ pixel), D is the size of the camera's pixels (in micrometers), and F is the focal length of the telescope (in mm). The use of this formula implies knowing exactly the values ​​of D and F. In the large observatories that data is determined with sufficient certainty, but with the instruments available to amateurs, the data provided by the manufacturers are not always reliable and can not be used if we want to do a job with a minimum of precision.

The solution is to obtain the resolution directly from the images. In the case of night images, the positions of the stars are compared with those of a catalog. There are many programs that correlate the distances of the catalog in seconds of arc with the distances in pixels of the images, deducting the resolution. In the case of the Sun, this can only be done with images of the entire disk, since this is the only element whose dimensions we can know a priori. The SOL program provides the radius of the disk (in seconds of arc and pixels) and the resolution for each observation day.

If the file with the spots positions and the "sol.lst" is retained, both generated by the program itself, it is possible to recover the data on the radius without having to reprocess the images. In the position file, the ephemeris for the day and hour of the observation appear at the end. The second input ("D =") corresponds to the solar diameter in arc seconds. In the file "sol.lst", the fourth line contains three numbers. The last one is the radius in pixels.

In the example that follows, a telescope with a theoretical focal length of 900mm and a camera with a pixel of 3.85m have been used. Although it is possible to use shorter intervals, the measurements made since the beginning of 2014 at the beginning of 2018 have been used.

The following graph shows the theoretical values ​​(sinusoidal blue line) and the radius values ​​obtained from the images, considering the focal lenght provided by the manufacturer (red dots). The latter have been adjusted by a sine function. The adjustment would be correct if the Earth's orbit were circular, but the difference is very small and hardly influences the result. On the other hand, the adjustment will be good if at least one cycle has been covered, so observations should be extended for at least one year. The horizontal lines indicate the theoretical average value and the adjustment value:

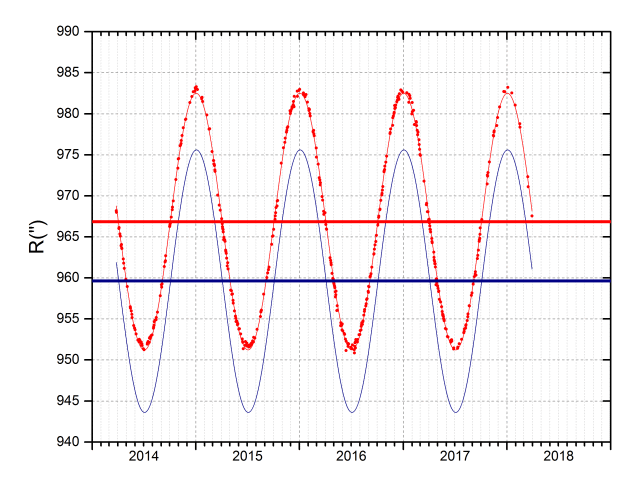
The difference between both curves, and their average values, means that the focal, the size of the pixels, or both, are not correct. A difference of 7" in the radius is not an optimal situation if we want a minimum of precision in our measurements, especially if the spots are relatively close to the limb, where errors can easily exceed 1º, due to this cause. Since we do not know how much error both parameters have, we are going to assume that the size of the pixels is correct, and that all the error accumulates in the focal. Therefore, the focal point we calculate will not be real, but instead represents the effective focal lenght to which we are working.

The effective focal lenght can be determined in the following way:

with the example data:

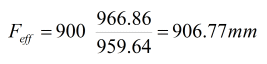
An alternative way of proceeding is to calculate the difference (dR) between the two radios each day. The result for the example, and its average value, is the one that appears in the graph:

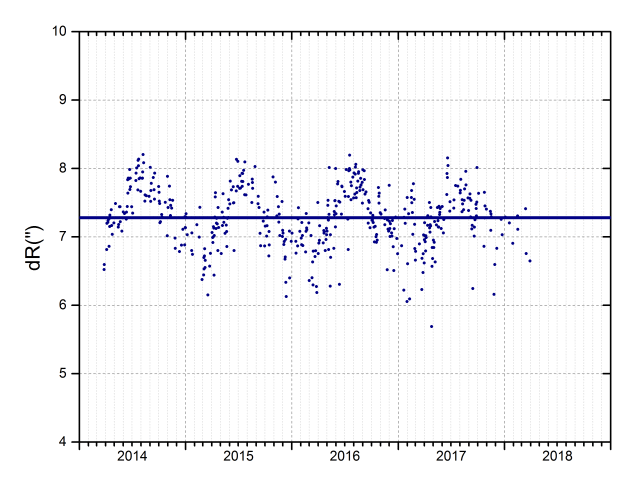
You can see an oscillation of annual character whose cause I do not have clear. Its amplitude makes the error associated with the focal is greater, but as the measures have been extended for 4 years, it is not relevant to the final result. As in the previous case, this is a reason to obtain the measurements for more than one year. The average value is 7.22" In this case, the effective focal lenght is:

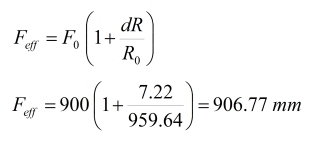
Finally, a small variation in the radius just means a variation in the resolution. In the previous example, the optical system has a resolution of 0.8757 "/ pixel, if we increase the radius by 0.4% (see article), the resolution becomes 0.8722" / pixel (0.4% lower), which means that when calculating areas, for example, it has practically no influence.

Javier Ruiz Fernández