The first detailed catalog on the most basic properties of the spots (positions and areas) was the Greenwich Observatory, which spans more than a century, from 1874 to 1976. At the end of its work in this field, the UAI commissioned the Debrecen Observatory the continuity of the program. Today is the indisputable reference when consulting sunspots positions. The measurements are made on images in white light obtained in Debrecen, and to complete the days not covered by Debrecen, images of other observatories are taken. The data can be accessed at the following link: http://fenyi.solarobs.csfk.mta.hu/DPD/

When comparing our series of data with that of Debrecen it is necessary to consider a difficulty. As the measurements have been made at different times, the movement of the spots themselves can generate a certain degree of dispersion. To avoid this problem we have used the set of spots with little proper motion that appears in the following list: http://www.parhelio.com/mp0.txt On the other hand, from the measures of Parhelio, those due to a single observer have been excluded, leaving those that result from averaging at least two observers. In total there are 450 positions.

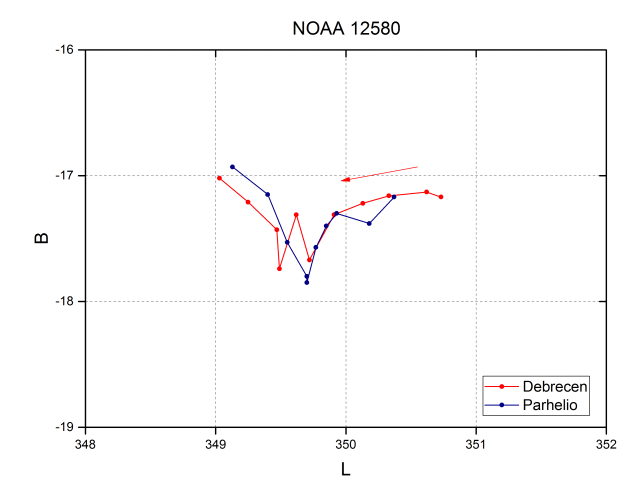
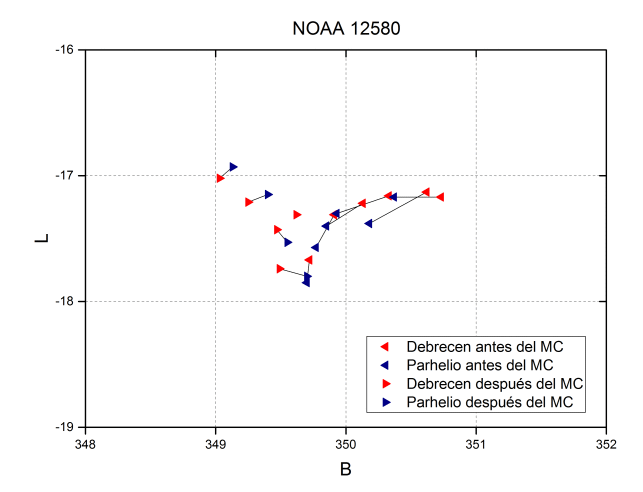
When representing the positions of individual spots the first thing we can verify is a good correspondence. For example, the NOAA 12580 graph where the arrow indicates the direction of movement. It should be noted that both in the Debrecen data and in ours, occasionally a certain dispersion is observed in the form of sudden jumps in the trajectory (they can be seen in the central positions in the graph). In our case, we measure the photometric center, but we do not know if what is measured in Debrecen is the geometrical or photometric center of the umbra. A variation in the shape or distribution of intensities of the umbra, as well as seeing, are factors that can contribute to these jumps. This dispersion has not been quantified, but the examination of the graphs suggests that the magnitude is similar in both series, so the influence of the aforementioned factors is similar.

To compare the two series, the distance D in degrees between the positions of Parhelio and Debrecen has been calculated as a function of the distance to the center of the disk expressed as a fraction of the radius of the disk. (Lp, Bp) are the coordinates measured by Parhelio and (Ld, Bd), measured by Debrecen. In these differences there is a contribution due to the aforementioned dispersion, which affects both series, so that in reality, the error produced by the measurement method itself would be less than calculated.

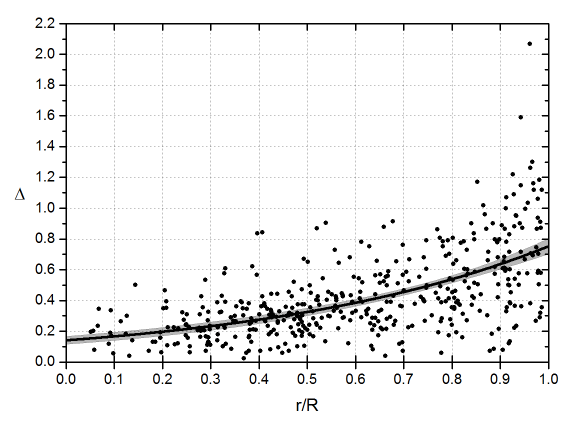
The graph shows the result. An adjustment has been added with an exponential function, and the corresponding confidence bands for a 95% probability.

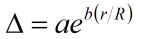
In the function, (a) is the ordinate at the origin, that is, the difference in the center of the disc, and (b) indicates the rate at which the difference grows as we approach the limbus. The values of the parameters are:

a = 0.14º ± 0.01º
b = 1.67º ± 0.11º

Because of a probabilistic issue (the spots take a short time to cross that area), in the center of the disk there are few measurements and the adjustment is less reliable, but the differences with Debrecen remain below 0.3º to almost half the radius, that it, a heliocentric angle of 30º; and below 0.5º to a heliocentric angle of about 50º (r / R = 0.77).

The magnitude D is the distance in a straight line between two positions, but if we calculate the distance in longitude and latitude separately and represent it as a function of the distance to the central meridian, a curious behavior appears. In principle, it would be expected that the data formed a cloud of points in the form of a horizontal band centered on Y = 0, that is, that the differences did not depend on the position of the spot on the disk, except for the greater dispersion that produces its proximity to limbo. However, as it can be seen, it is not like that.

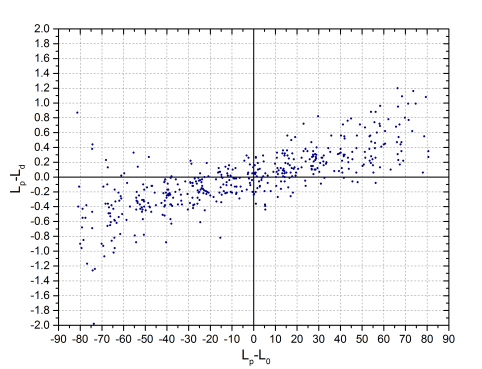
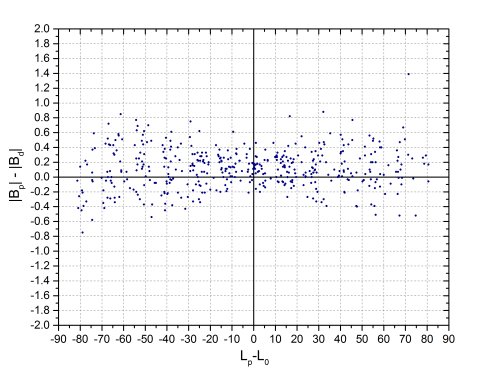
The first graph shows that when the spot is east of the meridian, our lengths tend to be smaller than those of Debrecen, that is, they are farther east. On the contrary, to the west of the meridian, our positions are to the west of those of Debrecen. In the graph to the right, to avoid visually compensating the differences of spots located in different hemispheres, we have not taken into account the sign, that is, it has been considered that all latitudes are positive. There the horizontal band appears, but it is not centered on the origin but displaced approximately 0.1º of it. The quantitative interpretation of this graph is complicated because the latitude of the center of the disk (B0) should be taken into account, but basically it tells us that, on average, our latitudes are slightly higher than those of Debrecen.

Both effects can be seen in the NOAA 12580 spot. The lines join the positions corresponding to the same days, and the orientation of the triangles indicates the location of the spot with respect to the meridian.

The solution to this small enigma is obtained by considering both graphs together. What they are telling us is that our positions place the spots closer to the limb than in the case of Debrecen ........ or the limb closer to the spots. In short, the radius of the disc that we have used is slightly smaller that of Debrecen.

When calculating positions, in principle radius can be used in two ways: we can use the value calculated from the ephemeris and the instrumental characteristics, or obtain it directly from the images. As explained in the previous article (http://www.parhelio.com/en/articulos/articresol.html), the first method is not recommended given the uncertainty with which we know the focal lenght and the size of the pixels.

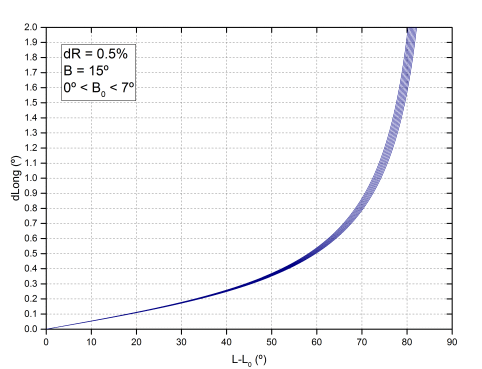
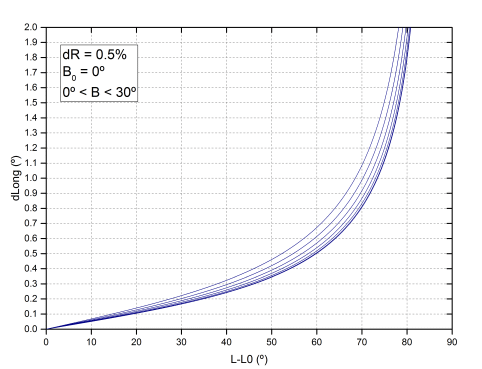
In order to see if we can deduce, even if it is approximately, what radius difference we have with Debrecen, we have to check how the coordinates vary, if we reduce a percentage of the radius. In the case of latitude, it always increases, which is what we checked previously. The way in which a variation of the radius is transmitted to the longitude is determined by a series of expressions that also depend on the latitude of the spot (B), and the latitude of the center of the disk (B0). The dependence with B0 and B is small. The following graphs represent what varies the longitude (dLong) as we move away from the meridian, assuming that we reduce the radius by 0.5%. In the first graph we assume that the latitude of the spot is 15º (average latitude of the spots analyzed) and we vary B0 between 0º and 7º. In the second we consider B0 = 0º, and we assume spots at different latitudes between 0º and 30º.

However, keeping the latitude and B0 fixed, the dependence on a variation of the radius is much higher. So for example, if we assume B = 15º and B0 = 0º, and we change the radius between 0.1% and 0.8%, the result is the following:

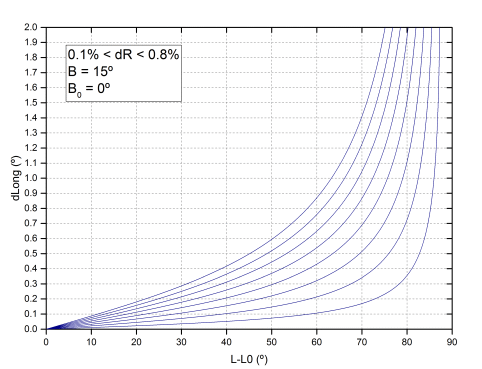
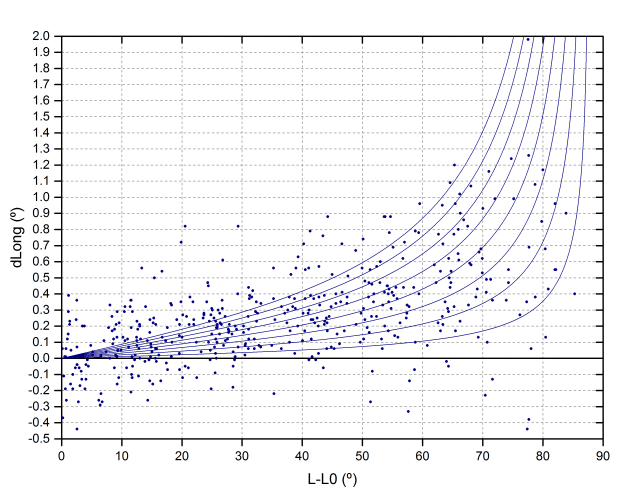
This graph is interesting because by superimposing it on the data we can have an approximate idea of what the difference is in the radius. Given the symmetry, we have passed all the data to the west of the meridian changing them of sign. Although the dispersion is very high, it seems that the best adjustment is obtained for values of dR around 0.4%.

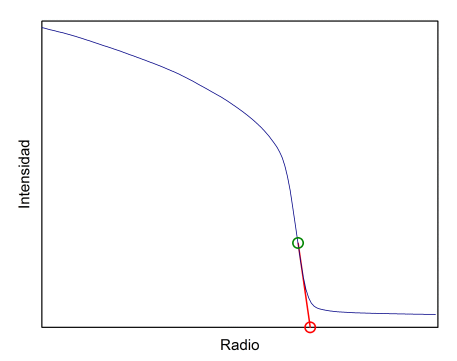
Taking into account that we do not know what is the method used in Debrecen, in principle we can imagine two causes for this difference in the radius. If we make a cut perpendicular to the limbus, the intensity decreases from the values inside the disk to the intensity of the sky background (see graph). The SOL program defines the limb as the inflection point of said brightness drop, that is, the point where the decrease is faster (green circle in the graph). It seems a logical choice given that, due to atmospheric diffusion and seeing, light is scattered on both sides of the limbus. However, it would also be possible to use some other method, such as cutting the X-axis of the tangent at the inflection point (red line and circle). Tests on several images suggest that this method could account for the 0.4% difference in radius.

Another effect to take into account, although it does not act in a systematic way, is the presence of very dark spots on the inside of the disc. Iris determines the radius by adjusting a circle to the pixels that have the intensity of the inflection point. When all these pixels are found along the limb, the adjustment is good, but if some spot is so dark as to reach that intensity, the program includes its pixels in the adjustment and the result is a circle of smaller radius. Since the 2017 version, SOL avoids this problem, but all the spots analyzed are earlier, so it is a factor that we can not rule out. The measures in the next years will confirm or not their influence.

Javier Ruiz

Bibliography
T. Baranyi, L. Gyóri, A. Ludmány: On-line Tools for Solar Data Compiled at the Debrecen Observatory and their Extensions with the Greenwich Sunspot Data, Solar Physics, 291, 3081-3102, 2016, DOI: 10.1007/s11207-016-0930-1
L. Gyóri, A. Ludmány, T. Baranyi: Comparative analysis of Debrecen sunspot catalogues, Monthly Notices of the Royal Astronomical Society, 465 (2), 1259-1273, 2017, DOI: 10.1093/mnras/stw2667
T. Baranyi: 2015, Comparison of Debrecen and Mount Wilson/Kodaikanal sunspot group tilt angles and the Joy's law, MNRAS, 447, (4): 1857-1865, doi:10.1093/mnras/stu2572